不怎么正规的前言:
《伤害输出》是我已经动笔写了接近一年的一部作品。但是很遗憾,整部作品计划有五章,我目前只完成了第二章。第一章因写作水平有限,怎么改都不满意,所以只能先放下。后面三章尚未开始。
如果按照这个进度,整部作品完成可能需要太久的时间,所以我打算先放出第二章的内容。第二章的内容是“解析评估方法”,讲的是如何用数学解析的方式来评估一个角色的DPS。
作品中带有[M]标志的内容表示里面用到了高等数学;带有[HM]标志的内容表示里面用到了专业性较强的数学。无论如何,作品中大量使用的数学符号是为了精确描述,我建议读者去尝试阅读这些符号,但如果读者感到厌烦,略过所有数学符号应当不会影响你理解文章内容。
如果有生之年能完成全部五章内容,我会重新把它们整理成一篇作品。
解析评估方法
从这一章开始,我们要开始介绍实际的方法了。我们首先从评估开始。评估要做的事情是在实际进行游戏之前估计(或者说计算)DPS,有了评估的能力,我们才能做到在战前调整好状态,做好最佳准备,意义不言自明。评估可以直接解决“N选1”的决策问题——你有两件装备不知道哪个好?分别评估一下就知道了。评估同样也是后面我们要探讨的优化问题的基础,所以也在解决“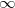 选1”规划问题中发挥不可替代的作用。
选1”规划问题中发挥不可替代的作用。
我们这里将评估方法分成了两大类:解析评估方法和统计评估方法。大家其实更熟悉统计评估方法,因为SimC属于统计评估,而且SimC的开发者们在哲学上是将解析评估和统计评估对立起来的,他们将这两类方法称为“Formulation”和“Simulation”[Ref]。如果听他们的说法,你会感觉“Simulation”是强大的而“Formulation”几乎没有意义。他们的说法其实大多都是对的,但一面之词春秋笔法,催使人产生主观情绪。这些开发者都是做实事的人而非理论家,统计方法更实用,所以当然更受到他们的青睐。
这里我将解析评估方法放在最一开始的位置,是因为我认为理解这类方法对于理解整个伤害输出问题的帮助是最大的,掌握这里的几个方法后读者会对整个问题有一个彻底颠覆的认识,所有人(只要你想认真玩)都应当了解这些方法。而之后还有对统计评估方法的介绍,则是因为统计方法确实在实际运用上更具有可行性,是供真正付诸研究实践的Theorycrafter准备的。
阅读这一章节读者要牢记,这些方法虽然能够解决问题,但我们大多数时候不会直接运用这些方法。讨论它们是为了分析和解剖我们的问题,所以读者应当着重理解每一个方法当中蕴含的思想。这里的每一个方法都是在经历相当精妙的思考后才能得到的,个个都让人拍案惊奇。
我想用实例的方式来叙述方法,我们需要构造一个例题,然后用各种方法求解它,并且在求解的过程中向读者展示这些方法的精妙之处。为了让大家不用花太多时间在理解例子上,对于评估和优化两类问题我都仅举一例。当然,例题是比较简单的,但它会包含实际问题当中碰到的那些难以处理的因素,所以实际问题无非就是将这些例题的规模扩大了而已,而求解方法几乎是完全相同的。
对于评估,我们将始终探讨这样一个问题:
笨牧师到目前为止暂时只会一个技能“痛”。

图 谁都会有搞砸的时候啦[Ref]
因为不熟练,笨牧师的痛只有30%概率会命中。
没命中的话,就什么都不会发生。如果命中,则挂一个DoT,每GCD造成1伤害,持续3GCD。如果重复挂DoT,会刷新。
在这里,为了方便起见,我们把时间的单位统一,无论GCD还是秒我们都认为是原子时间,而且干脆假设一个GCD就是1秒,以避免在时间单位上反复折腾。
笨牧师连续不停地对假人释放痛,求DPS期望。
这个问题非常经典,而且也相当实用,这个问题实际上来自于研究实践,而且在各个职业的模型当中都经常遇到它。举两例:
激怒覆盖率问题
狂暴战有一个技能叫嗜血。释放嗜血占用1GCD,如果嗜血暴击(几率为c%),战士会激怒,持续5GCD。战士每3GCD释放一次嗜血,求激怒覆盖率。
狩猎刺激问题
猎人不停地释放奥术射击。每次奥术射击有30%的概率触发狩猎刺激,使下三次奥术射击的集中值消耗降低10点(重复触发则回到3层)。求奥术射击平均每发节约了多少集中值。
战士用这个模型来估计精通的收益,猎人则用这个模型估计狩猎刺激天赋的价值,所有“触发效果覆盖率”相关的问题大多都是这种模型,可以说是WoW当中的常见问题了。会计算它应当说很关键。
这个问题说难也并不难,但大多数人独自解此问题都不容易想出来,需要经其他人点拨一下才能找到解法(否则当时就不会为此讨论那么多层楼了)。
我们求覆盖率。因为DoT的伤害是固定的,有了覆盖率我们很容易求DPS。
所谓覆盖率,有两种解释。一种是概率解释:假设笨牧师已经连续练习很久了,整个过程进入稳态,然后任取一个时刻看此时有DoT挂在木桩上的概率。一种是频率解释:让笨牧师打很长时间的木桩,然后统计DoT总共持续的时间,除以笨牧师打木桩的总时间。这两种解释最终得到的值是相同的(联系大数定律,它们相当于一个期望和均值的关系)。在实际游戏中,我们常用第二种,但分析问题时我们用第一种,因为分析问题的时候我们没有统计数据,而实际游戏中我们又懒得算。
问题的难点在于,当前时刻是否有DoT,与过往的事件有关。很难直接写出某一时刻有DoT覆盖的概率(假设为p),因为之前(3秒内)任何一个时刻触发DoT都会延续到当前时刻,然后重复触发又会掩盖先前的触发,所以你几乎无法从“当前时刻DoT覆盖”反推出关于历史的任何有用的信息。
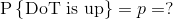
一点点逆向思维可以极大地简化这个问题。我们求“当前时刻DoT未覆盖”的概率。从“当前时刻DoT未覆盖”我们可以反推出有用的历史信息,因为当且仅当“前3次痛全部Miss”时,当前时刻才会“DoT未覆盖”。
命题“当前时刻DoT未覆盖”是“前3次痛全部Miss”的充分必要条件
充分性:命题“前3次痛至少有1次命中”→“当前时刻DoT覆盖”为真(显然),所以逆否命题“当前时刻DoT未覆盖”→“前3次痛全部Miss”也为真
必要性:“前3次痛全部Miss”→“当前时刻DoT未覆盖”(显然)
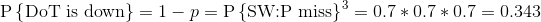
“当前时刻DoT未覆盖”的概率1-p,就是“3连Miss”的概率,就是“Miss”的概率的三次方。喔哦,这么想来好像很简单。
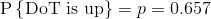
求DPS更简单,我们具体看某一个GCD。如果DoT覆盖了,则会造成1伤害;如果没覆盖就没有伤害。
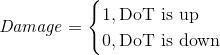
DPS是期望伤害除以时间。对这一个GCD求DPS就可以了,因为整个过程是由无数个像这样的GCD组成的,各个GCD之间都是对称的。(这种说法是通俗的直观解释,从马尔科夫链的角度来看,是因为这个链具有“非周期性”。)
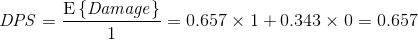
2012年3月,华中科技大学的黄志超第一个向我展示了此类问题的古典解法。
上一种解法虽然妙但并不美。隐约之中我们能够感觉到问题的全貌没有展示出来,而是被我们用小技巧回避了。我们找到了这个问题的一个弱点,然后从这一点突破,解决了这个问题,然而并不是所有问题都会有这样的弱点供我们突破。我们需要更加有力的工具来解决更广泛的问题,所以这一回,我们迎难而上,全面解剖问题,而不是寻求捷径。
在任意时刻,笨牧师可能处于以下四种状态之一(断痛,1/3痛,2/3痛,满痛),我们分别标记为 。在刚才的解法中,我们是以
。在刚才的解法中,我们是以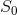 作为突破口的。
作为突破口的。
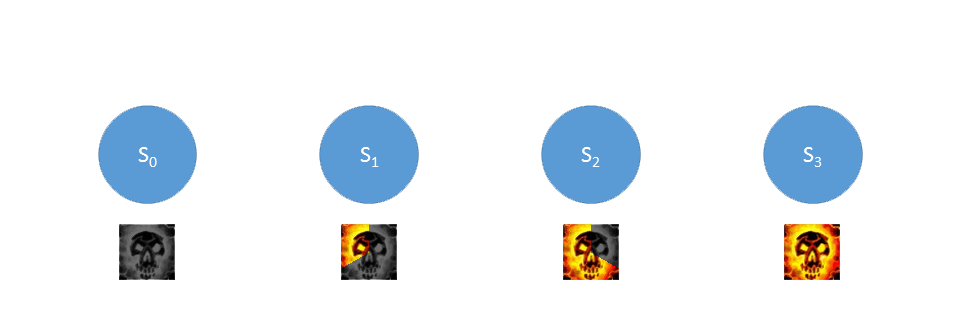
图 状态划分
每次施法,都会导致状态发生转移:
处在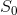 时,下一步有30%的概率转移到
时,下一步有30%的概率转移到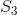 (命中),有70%的概率转移到
(命中),有70%的概率转移到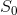 (未命中)。
(未命中)。
处在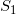 时,下一步有30%的概率转移到
时,下一步有30%的概率转移到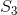 (命中),有70%的概率转移到
(命中),有70%的概率转移到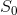 (未命中)。
(未命中)。
处在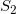 时,下一步有30%的概率转移到
时,下一步有30%的概率转移到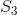 (命中),有70%的概率转移到
(命中),有70%的概率转移到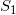 (未命中)。
(未命中)。
处在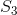 时,下一步有30%的概率转移到
时,下一步有30%的概率转移到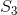 (命中),有70%的概率转移到
(命中),有70%的概率转移到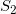 (未命中)。
(未命中)。
这是很容易列写的。导致状态转移的因素有两个,一个是痛的命中与否,一个是时间的流逝,不要忘记后面这个因素,时间推移导致你在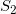 打出Miss会流逝到
打出Miss会流逝到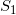 。
。
我们把状态转移画到图上。
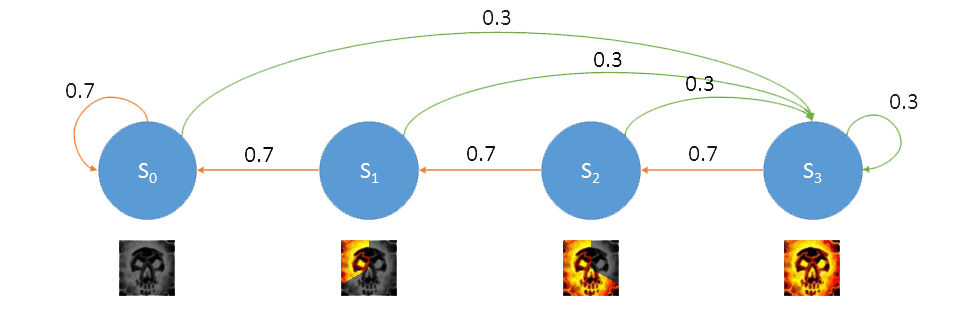
图 马尔科夫链
图中绿色箭头表示命中的结果,红色箭头表示未命中的结果。它们的转移概率分别写在了连线上。至此,我们构建了一个每条边都带有概率的有向图,这就是一个完整的马尔科夫链。
人们关于马尔科夫链的研究已经进行了上百年,所以我们将问题转化成了一个马尔科夫链之后,我们就有丰富的理论工具来对付这个问题了。在上一个解法中,我们求的是“痛的覆盖率”,这里我们也可以很容易地求覆盖率,我们运用马尔科夫链当中的“平稳分布”这个工具来求。
平稳分布指的是,当马尔科夫链平稳后(平稳指已经进行了很多步转移,记不清最开始是从哪里出发的了),任意时刻我们处在各个状态上的概率。我们假设平稳分布为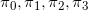 ,分别表示我们处在
,分别表示我们处在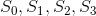 状态上的概率。
状态上的概率。
我们知道我们一定处于这四个状态中的一个,所以有
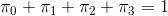
因为整个过程已经平稳,当前我们的分布是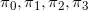 ,那么进行一步状态转移后新的分布应当仍然是
,那么进行一步状态转移后新的分布应当仍然是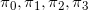 。据此可以列写方程组
。据此可以列写方程组
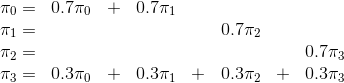
每一个方程的含义都是“此状态的分布=转入此状态的概率之和”。
将以上方程联立求解,可以得到
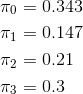
这个结果的含义是:任意时刻没有痛的概率是0.343,痛持续时间剩余1秒的概率是0.147,持续时间剩余2秒的概率是0.21,持续时间剩余3秒的概率是0.3。覆盖率是“有痛的概率”即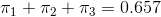 。这样我们就回到了上一个方法的最后一步。
。这样我们就回到了上一个方法的最后一步。
我们能不能不通过覆盖率计算DPS,而是直接从马尔科夫链的工具出发求出DPS呢?毕竟并不是每一个伤害输出问题都是无限挂DoT这样简单的,遇到复杂的问题没有通用的解决办法而只会取巧就会很麻烦。上面我们在建模时一直忽略了一个重要的因素:伤害。伤害作为一种价值取向,我们应当以“回报”的形式加入到模型中来,也就是说,造成伤害是对我们角色的一种奖励。将回报值写在每一条边上,就形成了我们完整的马尔科夫模型。
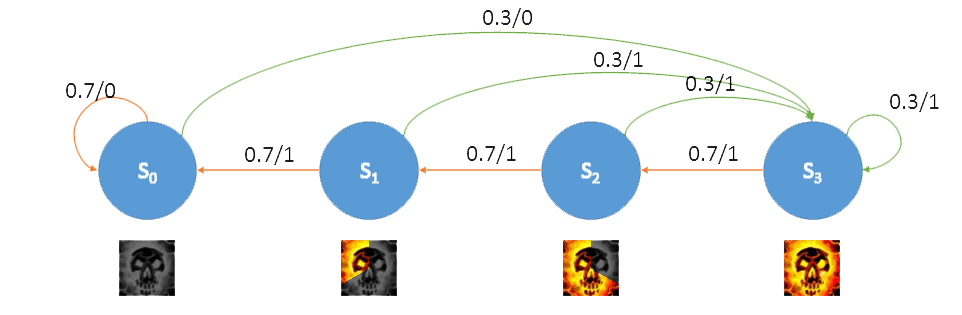
图 添加了回报的马尔科夫链
在笨牧师问题里,只要处于有痛的状态,就会造成1点伤害,所以我们把从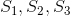 转移出去的边加上回报值1,把从
转移出去的边加上回报值1,把从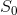 转移出去的边加上回报值0。注意到每当离开状态
转移出去的边加上回报值0。注意到每当离开状态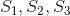 时总会造成1点伤害,而离开
时总会造成1点伤害,而离开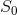 时不会造成伤害,所以可以依平稳分布加权求得DPS
时不会造成伤害,所以可以依平稳分布加权求得DPS
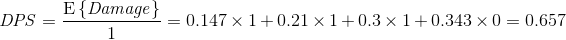
马尔科夫链清晰地描述了问题模型,并且也很容易求解,接下来有许多方法将基于马尔科夫链构建,所以理解此方法中的状态划分和状态转移的思想非常重要。
2013年8月,在探讨一个类似的问题(狩猎刺激)时,llxibo给出了一份基于马尔科夫链的解法[Ref]+得到了与古典解法相同的结果,并扩充了可解的问题范围。
在NGA能够找到一些年代非常古老的运用马尔科夫链的帖子,说明这个工具很早就已经有人在使用了。我在每个方法后面附注的来源,都是我自己得到这些方法的来源,而不是这些方法的创始。
热门资讯
HOT NEWS
热门视频
HOT VIDEOS
原创推荐
Original